6 Essential Quadrilateral Shapes to Know About!

Shapes are all around us, from the pages of our books to the buildings we live in. Quadrilateral shapes can often be confusing.
In this guide, we’ll explore six important shapes that make up much of our world: squares, rectangles, parallelograms, rhombuses, trapeziums (also known as trapezoids), and kites.
These shapes aren’t just ideas in math books—they’re part of our everyday lives.
We’ll examine what makes each shape special, how to determine its sizes and edges, and where we see it in real life.
Whether you’re a student trying to understand geometry better or just someone curious about the world around you, this guide will help you see these shapes differently.
Let’s discover how these simple forms create our complex world.
List of Quadrilateral Shapes You Should Know
1. Square

A square is a quadrilateral with equal sides and all angles at 90 degrees. It is a regular polygon with symmetrical properties.
- Properties: All sides are equal. Diagonals are equal, bisect each other at right angles, and are perpendicular.
- Area: Area = a × a
- Perimeter: Perimeter = 4 × a (where ‘a’ is the length of a side)
- Real-world examples: Squares are prevalent in urban planning and modern architecture, where symmetry and balance are essential.
2. Rectangle

A rectangle is a quadrilateral with opposite sides equal and all interior angles right angles.
- Properties: Opposite sides are parallel and equal. Diagonals are equal and bisect each other.
- Area: Area = length × width
- Perimeter: Perimeter = 2 × (length + width)
- Real-world examples: Most doors, books, and smartphones are rectangular, utilizing the shape’s straightforward and efficient design.
3. Parallelogram

A parallelogram is a quadrilateral where opposite sides are parallel.
- Properties: Opposite sides are equal and parallel; opposite angles are equal. Diagonals bisect each other but are not necessarily equal.
- Area: Area = base × height
- Perimeter: Perimeter = 2 × (base + side length)
- Real-world examples: Bridges often incorporate parallelogram components to distribute forces evenly.
4. Rhombus
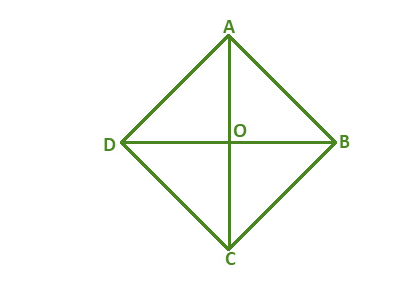
A rhombus is a parallelogram with all four sides of equal length.
- Properties: All sides are equal. Diagonals are perpendicular to each other and bisect the angles of the rhombus.
- Area: Area = (diagonal₁ × diagonal₂) ÷ 2
- Perimeter: Perimeter = 4 × side length (where ‘diagonal₁’ and ‘diagonal₂’ are the lengths of the diagonals)
- Real-world examples: Rhombuses are featured in tiling patterns and jewelry, providing aesthetic appeal through their symmetrical geometry.
5. Trapezium (Trapezoid)

A trapezium has at least one pair of parallel sides, known in the U.S. as a trapezoid.
- Properties: Only one pair of parallel sides. The height is the perpendicular distance between these sides.
- Area: Area = [(base₁ + base₂) × height] ÷ 2
- Perimeter: Perimeter = base₁ + base₂ + side₁ + side₂ (where ‘base₁’ and ‘base₂’ are the lengths of the two parallel sides)
- Real-world examples: Many bridges and roof trusses use the trapezium shape for structural stability and aesthetic value.
6. Kite

A kite has two pairs of adjacent sides that are equal.
- Properties: Diagonals intersect at right angles. One diagonal bisects the other.
- Area: Area = (diagonal₁ × diagonal₂) ÷ 2
- Perimeter: Perimeter = 2 × (side₁ + side₂) (where ‘side₁’ and ‘side₂’ are the lengths of the distinct pairs of adjacent sides)
- Real-world examples: The traditional flying kite mimics this geometric shape, exploiting its aerodynamic properties.
Summing Up
As we’ve seen, these six shapes – squares, rectangles, parallelograms, rhombuses, trapeziums, and kites – are more than just lines on paper.
They’re the building blocks of our world, from the tiniest microchip to the grandest skyscraper.
Understanding these shapes helps us make sense of the world around us. It can improve our problem-solving skills, help us appreciate art and architecture, and even inspire new ideas in design and engineering.
Knowledge of these shapes can be surprisingly useful, whether for planning a garden, arranging furniture, or just looking at the world with fresh eyes.
Remember, geometry isn’t just for mathematicians—it’s a tool for better understanding and interacting with our environment.
So, next time you’re out and about, take a moment to spot these shapes in action!
Frequently Asked Questions
1. What is the Difference Between a Square and A Rhombus?
All squares are rhombuses with right angles, but not all rhombuses are squares. The key difference lies in their angles:
- Square: All interior angles are right angles (90 degrees). It is equilateral (equal sides) and equiangular (equal angles), making it a regular quadrilateral.
- Rhombus: Opposite angles are equal but not necessarily 90 degrees. The sides are equal, but the angles can vary, making the shape more “slanted” than a square.
2. How can I Determine if a Quadrilateral is a Parallelogram?
A quadrilateral is a parallelogram if it meets any of the following conditions:
- Opposite Sides are Equal and Parallel: Both pairs of opposite sides are equal in length and parallel.
- Opposite Angles are Equal: Both pairs of opposite angles are equal.
- Diagonals Bisect Each Other: The diagonals cut each other exactly in half.
- One Pair of Opposite Sides is Equal and Parallel: If even one pair of opposite sides is equal and parallel, the quadrilateral is a parallelogram.
3. Can a Trapezium (trapezoid) have Right Angles?
Yes, a trapezium (known as a trapezoid in North America) can have right angles. When a trapezium has two right angles, it is specifically called a right-angled trapezium or right trapezoid.






